Validity, Strength, Soundness and Cogency
From Logic
(→Validity) |
|||
| Line 16: | Line 16: | ||
To get a clearer idea of what "preserving truth" in arguments really means, consider the idea of a set of directions designed to get you to a destination - a road map. Imagine you have a set of directions on how to get to from Soho to Little Italy. | To get a clearer idea of what "preserving truth" in arguments really means, consider the idea of a set of directions designed to get you to a destination - a road map. Imagine you have a set of directions on how to get to from Soho to Little Italy. | ||
| - | + | http://i602.photobucket.com/albums/tt102/hanniballecturer/candleinthedark/roadmap-4.gif | |
| - | http://i602.photobucket.com/albums/tt102/hanniballecturer/candleinthedark/roadmap.gif | + | |
We will consider you and your car to represent the "Truth" and we will consider the roads as "premises", and your final destination as the "conclusion" that your car/the truth, want to reach to support your argument. | We will consider you and your car to represent the "Truth" and we will consider the roads as "premises", and your final destination as the "conclusion" that your car/the truth, want to reach to support your argument. | ||
| Line 51: | Line 50: | ||
For this reason, it is important to make sure that we use the term "valid" only to refer to arguments that have the proper form - arguments that give proper directions to the conclusion, while remembering that proper form means nothing if we have false premises. Validity has to do with the form, and 'Truth" has to do with examining the individual premises, Both invalid and valid arguments can contain either true of false premises, in fact, of the 8 possible permutations between true and false premises and true and false conclusions in valid and invalid arguments, there is only one set of premises and conclusions we will not see: a set of ALL true premises with a false conclusion. To best represent all the possible permutations, I've replicated two tables from Copi's Introduction to Logic (10th Edition): | For this reason, it is important to make sure that we use the term "valid" only to refer to arguments that have the proper form - arguments that give proper directions to the conclusion, while remembering that proper form means nothing if we have false premises. Validity has to do with the form, and 'Truth" has to do with examining the individual premises, Both invalid and valid arguments can contain either true of false premises, in fact, of the 8 possible permutations between true and false premises and true and false conclusions in valid and invalid arguments, there is only one set of premises and conclusions we will not see: a set of ALL true premises with a false conclusion. To best represent all the possible permutations, I've replicated two tables from Copi's Introduction to Logic (10th Edition): | ||
| - | + | ||
<center> | <center> | ||
| Line 101: | Line 100: | ||
</table> | </table> | ||
</center> | </center> | ||
| - | </ | + | </center> |
== Soundness == | == Soundness == | ||
Revision as of 21:03, 28 March 2010
 In assessing a deductive argument, we must first determine whether it is valid.
In assessing a deductive argument, we must first determine whether it is valid.
Contents |
Validity
Validity has to do with the formal characteristics of an argument, whether the propositions in the argument preserve the truth along the premises to the conclusion. For example, consider this valid argument - a hypothetical syllogism:
Premise 1: If A is true, then B is true Premise 2: If B is true, then C is true Conclusion: Therefore, if A is true, then C must be true
Here we can see that the truth of premise 1 is is carried over, or preserved in premise 2, through the the fact that term B appears in both premises. The use of this repeated term connects premise 1 and premise 2 together. Provided A is true, then the truth of A is carried through each premise to the conclusion. The conclusion only contains propositions contained in the premises that were connected by the connecting term "B", so we know that the conclusion must necessarily follow from the premises, and must, necessarily, be true if proposition A is true.
A deductive argument therefore, is valid if and only if the conclusion must necessarily follow from the premises. So we may test a deductive argument for validity by checking to see if there is any possibility that the premises could be true and the conclusion false. If so, the form of the argument must be invalid, there must be a place where the 'truth" of the propositions is not being carried through to the conclusion.
To get a clearer idea of what "preserving truth" in arguments really means, consider the idea of a set of directions designed to get you to a destination - a road map. Imagine you have a set of directions on how to get to from Soho to Little Italy.
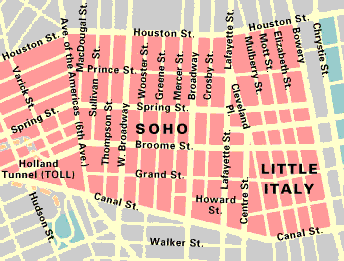
We will consider you and your car to represent the "Truth" and we will consider the roads as "premises", and your final destination as the "conclusion" that your car/the truth, want to reach to support your argument.
If I told you to start out from Soho by taking Broome Street towards Lafayette (at the center of the map) and then to turn right down Mulberry Street (look for the name at the top right of the map), each step would take YOU along the path to your destination, Little Italy. We would "preserve the truth" by carrying you along the roads/premises, by getting you to your destination/conclusion!
However, if I told you instead to turn left onto Lafayette, you would end up lost. You'd never reach your destination. The invalid set of directions - or a invalid set of premises , wouldn't allow you to reach the destination, or conclusion - even though your destination, Little Italy, is still a real place.
When we say that an argument is invalid, nothing is necessarily being said about the truth value of the premises or even the truth value of the argument's conclusion. As David Coss states, all that is being said when we declare an argument to be invalid is that the argument does not support its conclusion, because the argument does not preserve truth value through all the premises, to the conclusion. Or, using our example from above, the directions don't get you to your destination, even though the destination actually does exist.
At the same time, a valid argument does not necessarily mean that the conclusion is true! Using our example from above, I could tell you that by taking Broome street to Mulberry, you will end up at China Town - the directions would take you to the place I wish to direct you to, but I would be wrong about the destination. This means that at least one of my premises must be false.
Copi, in his Introduction to Logic (10th Edition), presents a classic example of this point: "This point was made forcibly by Abraham Lincoln in one of his debates with Stephen Douglas, in 1858. Lincoln was attacking the Dred Scott decision, which obliged the return of slaves, who had escaped into northern states, to their owners in the south:
"(I believe the following) syllogistic argument... follows (from The Dred-Scott decision), and submit it to the consideration of men capable of arguing whether... the argument has any fault in it: Nothing in the Constitution or laws of any state can destroy a right distinctly and expressly affirmed in the Constitution of the United States. The right of property in a slave is distinctly and expressly affirmed in the Constitution of the United States. Therefore, nothing in the Constitution or laws of any state can destroy the right of property in a slave. I believe that no fault can be pointed out in that argument (i.e., it is valid); (AND) assuming the truth of the premises, the conclusion, so far as I have capacity at all to understand it, follows inevitably. There is a fault in it as I think, but the fault is not in the reasoning, but the false-hood in fact is a fault of the premises. I believe that the right of the property in a slave is not distinctly and expressly affirmed in the Constitution, and Judge Douglas thinks it is. I believe that the Supreme Court and the advocates of that decision may search in vain for the place in the Constitution where the right of property in a slave is distinctly and expressly affirmed. I say, therefore, that I think one of the premises is not true."
For this reason, it is important to make sure that we use the term "valid" only to refer to arguments that have the proper form - arguments that give proper directions to the conclusion, while remembering that proper form means nothing if we have false premises. Validity has to do with the form, and 'Truth" has to do with examining the individual premises, Both invalid and valid arguments can contain either true of false premises, in fact, of the 8 possible permutations between true and false premises and true and false conclusions in valid and invalid arguments, there is only one set of premises and conclusions we will not see: a set of ALL true premises with a false conclusion. To best represent all the possible permutations, I've replicated two tables from Copi's Introduction to Logic (10th Edition):
 I met a Texan once who wore a goofy hat. I bet all Texans wear goofy hats.
I met a Texan once who wore a goofy hat. I bet all Texans wear goofy hats.
